Roulette - La montante a riduzione logica - Roulette Amica

(g.paludi) Francar, ossia Franco Carrarelli di Pordenone, fu un ludologo molto preparato e stimato. Morì troppo presto, ma lasciò comunque sistemi e studi che certamente andrebbero conosciuti da chi si interessa a questa affascinante materia. Ne presento uno particolarmente interessante come omaggio ad un amico che ricordo spesso con grande nostalgia.

Qualunque gioco sistemistico che preveda un utile entro un numero ragionevole di colpi sulle chances multiple, impiega una montante e, fra tutte, la montante Fibonacci sembrerebbe essere la migliore.
Questa montante è ricavata dal famoso triangolo cinese, da altri conosciuto con il nome di triangolo di Tartaglia ed ha un'unica regola: ogni termine successivo è determinato dalla somma dei due termini immediatamente precedenti.
La montante inizia col primo termine che sarà 1 pezzo; se questo termine è perduto, il secondo termine della montante sarà ancora 1, perché inizialmente non abbiamo termini immediatamente precedenti da sommare o meglio sotto l'unità abbiamo solo lo zero, e quindi 0 + 1 = 1 e con ciò abbiamo rispettato la regola.
Il terzo termine sarà uguale alla somma dei due termini precedenti e cioè 1 + 1 = 2.
Il quarto termine sarà uguale ala somma dei due termini precedenti e .cioè 1 + 2 = 3 e così di seguito formeremo la seguente colonna di termini

1
1
2
3
5
8

dove è facilissimo vedere che ogni termine successivo è uguale alla somma dei due termini immediatamente precedenti.
Naturalmente questa montante può proseguire all'infinito, ma ben presto ci accorgeremo come oltre un certo limite non possiamo andare, non fosse altro che per i massimi consentiti.
Si tratta di una montante in perdita (aumenta di valore con i colpi persi) che però prevede al primo colpo vinto il recupero del capitale impiegato oltre ad ottenere un certo utile, che aumenta gradatamente con l'aumento delle poste.
Tra le montanti che perseguono l'obiettivo di recuperare lo scoperto con un unico colpo di vincita, la Fibonacci è la migliore tra quelle conosciute, però dopo dieci colpi persi il nostro passivo è già di 143 pezzi.
Ora la domanda che ci viene spontanea è questa: siccome evidentemente qualunque nostro gioco subirà fatalmente delle fasi negative, ci conviene che il nostro scoperto aumenti sempre di più per poter guadagnare proporzionalmente di più, oppure ci conviene puntare di meno, accontentandoci di recuperare lo scoperto e conseguire il minimo utile di 1 pezzo, impiegando un capitale notevolmente inferiore?
Credo che qualsiasi persona di buon senso abbia già scelto la seconda ipotesi.
In questo caso possiamo adoperare una sola montante: la montante a riduzione logica.
La tecnica di questa montante è facile perché basterà fare un'elementare divisione per avere il valore della puntata da fare: capitale esposto diviso il premio pagato dal banco per la combinazione che giocheremo.
Se ad esempio stiamo perdendo 15 unità e per il prossimo colpo intendiamo giocare una dozzina, la nostra divisione sarà la seguente:

15 (capitale esposto) : 2 (premio pagato dal banco per le dozzine) = 7,5

nel caso che la divisione dia un resto, si arrotonda sempre per eccesso.
La puntata da fare sarà quindi 8 e se il colpo è favorevole incasseremo 16 pezzi di cui 15 recuperati e 1 pezzo di vincita.

Facciamo ora il confronto fra la Montante Fibonacci e la Montante a riduzione logica.

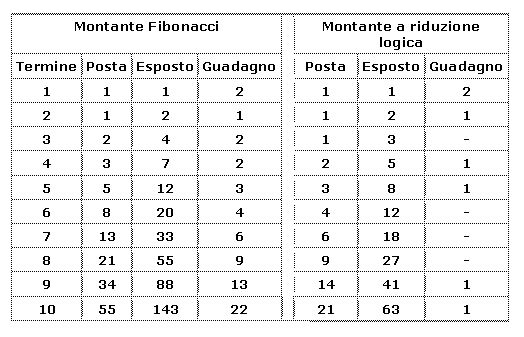
Il commento appare superfluo perché al posto di 143 pezzi di scoperto al decimo colpo della Montante Fibonacci, fa riscontro uno scoperto di soli 63 pezzi della Montante a riduzione logica e ciò che più conta abbiamo ottenuto ugualmente lo scopo del rientro del capitale in una fase di gioco avversa. Ecco spiegato il motivo per cui in precedenza avevo criticato la pur ottima Montante Fibonacci.

Siccome questa montante può essere adoperata per tutte le chances multiple riportiamo qui sotto la tabellina sintetica per il calcolo delle poste:

Come si è già detto, in caso di resto, si arrotonda il quoziente per eccesso.
Anche questa montante può essere impiegata per scaglioni e lo scoperto con essa sarà sempre inferiore a qualsiasi altra montante impiegata. Altro grosso pregio di questa montante è che non ha bisogno di macchinose registrazioni sul carnet di gioco, perché basta di volta in volta sommare lo scoperto (o le perdite in pezzi subite, se preferite) e dividere il tutto per il valore del premio della combinazione che andremo a giocare.
Naturalmente è possibile il gioco multiplo cioè puntare indifferentemente su dozzine, carrè, pieni, cavalli, colonne ecc.

Esempio
Supponiamo di avere uno scoperto di 7 pezzi. Se giochiamo una dozzina la nostra puntata sarà:
7 : 2 = 3,5, cioè puntata 4. Si perde, scoperto 11.
A questo punto giocheremo un carrè: 11 : 8 = 1,… puntata 2. Si perde, scoperto 13.
Giochiamo un cavallo:
13 : 17 = 0, puntata 1. Si perde scoperto 14.
Puntiamo un pieno:
14 : 35 = 0, puntata 1 si perde, scoperto 15.
Puntiamo una colonna: 15: 2 = 7,5, puntata 8.
Finalmente vinciamo un colpo utile e con esso recuperiamo lo scoperto di 15 pezzi, ottenendo anche 1 pezzo di guadagno e ci siamo divertiti a puntare sulla combinazione che più ritenevamo idonea ad uscire per il colpo giocato.
Concludendo, questa montante a riduzione logica può essere impiegata anche in continuazione sulle combinazioni che di volta in volta il nostro intuito o qualsiasi metodo ci suggeriscono e non possiamo assolutamente perdere perché ci basta un solo colpo vincente su una qualsiasi combinazione giocata per recuperare interamente lo scoperto, ottenendo il più delle volte un piccolo guadagno in una fase negativa. Il guadagno più consistente ci verrà invece da tutte le fasi del gioco per noi positive.